컴퓨터 구조 :: Cache 메모리

[컴퓨터 구조]Cache

Memory

  • 메모리란 크면 느리고, 빠르면 작을 수 밖에 없는 운명적인 한계를 갖습니다.
  • 느리면 가격이 저렴하기 때문에 크게 구성할 수 있고, 빠르면 가격이 비싸기 때문에 작게 구성해야 하는 경제적인 이유가 있고
  • 작은 메모리는 CPU와 가깝게 둘 수 있고, 큰 메모리는 CPU로 부터 멀리 두게 되는 지역적인 이유로 인한 속도 저하도 있을 것 입니다.

메모리의 한계

  • 메모리는 위에서 설명한 것처럼 하나가 길면 다른 하나가 짧아지는 운명적인 한계를 갖습니다.
  • 또한 CPU의 성능이 지수적으로 증가했음에도 메모리 Access spped는 1차함수로 증가하여 CPU의 성능과 상당한 격차가 벌어지게 됩니다.

우리가 원하는 메모리

  • 하지만 우리는 크고 빠른 메모리를 원합니다.
  • 메모리의 한계를 극복하고 사용자에게 크고 빠른 메모리처럼 보이도록 하기 위해서 만들어 낸 것이 메모리 hierarchy입니다.

Memory Hierarchy

  • Memory Hierarchy란 빠르고 작은 메모리와 크고 느린 메모리의 장점을 조합해서 크고 빠른 듯 행동하는 메모리를 만드는 것입니다.

구글 검

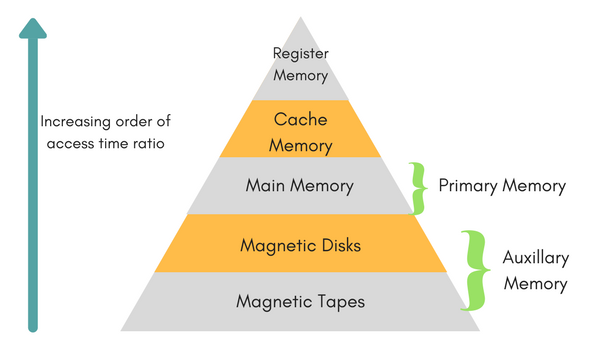
  • 우리는 앞으로 배울 Locality와 Cache를 사용해서 좋은 메모리 구조를 만드는 법을 배울 것입니다.

Locality

  • 지역성이란 컴퓨터는 최근에 썼던 주소와 동일한 주소나 주변의 주소를 다시 참조하는 경우가 자주 있다는 의미입니다.
  • Temporal Locality : 최근에 참조된 주소는 가까운 미래에 다시 쓰일 확률이 높다.
  • Spatial Locality : 방금 참조된 주소의 주변 주소들은 가까운 미래에 쓰일 확률이 높다.

Cache

  • Cache는 아키텍쳐 Set의 핵심 구성요소로 수나 크기를 변경하기 힘든 레지스터 메모리를 제외하고 그 다음으로 빠른 메모리입니다.
  • 앞으로는 크게 Cache와 Memory라는 두 개의 계층구조로 나누어서 Cache는 작지만 빠른 메모리, SlowMemory는 크지만 느린 메모리로 약속하고 얘기하려고 합니다.

Cache hit

  • CPU가 값을 가져오려고 할 때 Cache에 해당하는 값이 있다면 Memory까지 가지 않고 Cache까지만 가서 값을 가져올 수 있습니다. 이 경우를 Cache Hit이라고 합니다.

Cache Miss

  • 반대의 경우로 CPU가 값을 가져오려고 할 때 Cache에 해당하는 값이 없다면 Memory까지 가서 값을 가져와야 합니다. 이 경우를 Cache Miss이라고 합니다.
  • 그림은 12가 cache에 없는 경우에 메모리에서 가져오는 것을 보여주고 있습니다.

Cache를 어떻게 구성할까.

  • 만약 우리가 Cache메모리를 처음 고안해낸 사람이라고 생각해 봅시다. 우리가 쓰는 메모리 주소가 64비트로 이루어져 있고 각 메모리의 주소에는 1비트의 정보를 담을 수 있다고 가정해 봅시다. 한 칸의 메모리에 얼마의 정보를 담으면 효율적일지 고민하려고 합니다.

1비트씩 저장하기

  • 한 칸의 캐쉬 메모리에 1비트의 값을 저장한다면 8개의 비트의 값을 저장하기 위해서 캐시 메모리는 8개의 주소를 지니고 있는 방법을 쉽게 생각해 볼 수 있습니다.
  • 그렇다면 우리는 1Byte의 정보를 저장하기 위해서 8Byte 주소가 8개 필요합니다. 즉 주소를 저장하는 데에만 64Byte의 비트가 필요합니다. 너무 비효율적이죠?

8비트씩 저장하기

  • 조금 더 발전해서 8비트씩 값을 저장하면 어떨까요. 64비트에서 끝의 3비트는 모두 0으로 생각해서 주소로 61비트만 있다면 한 칸의 캐쉬 메모리에 8비트의 정보를 저장할 수 있을 겁니다.
  • 2^3 = 8이라는 걸 기억해서 64 - 3 = 61 비트가 성립했다는 것을 알면서 따라온다면 똑똑한 학생입니다.

2^b 비트를 저장하기

  • 왜 b라고 했을까요. 이유는 우리가 지금까지 한 칸이라고 불렀던 메모리의 한 칸을 블록(Block)이라고 하기 때문입니다.
  • 하나의 블록에 2^b비트를 저장한다면 우리에게 필요한 주소 비트는 몇 비트가 될까요.
  • 답은 64 - b 비트 입니다.
  • 자 여기까지 하고 간단한 예를 들어서 적용해 봅시다.

메모리 1000…001를 찾아주세요.

  • 우리가 만든 캐쉬 메모리는 한 블록에 2^b 비트를 저장할 수 있습니다. 그리고 아직 한 블록밖에 없다고 문제를 간단히 해보죠.
  • CPU가 1000…001이라는 64비트의 메모리 주소에서 값을 찾아달라고 요청합니다.
  • 그러면우리는 주소값에서 뒤에 b개의 비트를 제외한 64-b비트만 가져와서 우리의 캐쉬 주소와 비교해봅니다.
  • 운이 좋아서 해당 주소가 우리 캐쉬 주소와 일치했다고 합니다. 그런데 우리는 2^b의 비트가 있는데 어떻게 값을 찾을 수 있을까요.
  • 답은 우리가 방금 제외한 b개의 비트로 찾을 수 있습니다. b개의 비트의 값은 0…001이고 값이 1이라고 합니다. 그렇다면 우리는 0번부터 2^b번까지 가지고 있는 블록 데이터에 1번째 값을 찾으면 원하는 값입니다.
  • 0번째에서 얼마나 떨어져있는지 알려주는 b개의 비트를 BlockOffset이라고 부릅니다.

확장하기

  • 우리는 한 칸 짜리 캐시 메모리를 만들어 보았습니다. 그런데 이제 칸을 더 늘이고 싶습니다.
  • 조금 속도를 내 보겠습니다. 우리는 2^s개의 칸을 만들고 싶다고 해보죠. 그리고 이제 각각의 칸을 set이라고 부르겠습니다.
  • 2^s을 표현하려면 몇 개의 비트가 필요할까요. 네 s개의 비트가 필요한데요. s개의 비트를 set의 주소를 찾는데 쓴다면 우리의 캐쉬 주소 비트 = 64 - s - b로만 구성된다는 걸 알 수 있습니다.
  • 0번째 set에서 얼마나 떨어져있는지 알려주는 s개의 비트를 setOffset(index)이라고 합니다.
  • 우리가 지금까지 설명했던 캐쉬 주소란 tag비트라고 부릅니다. 메모리 주소가 cache에 있는지 비교하는 가장 결정적인 Key랍니다.

정리

  • Tag bit = 64 - s - b 비트라고 했습니다. 엄밀하게 설명하면 이전까지의 설명이 맞습니다.
  • 하지만 보통 캐시 메모리에 저장하는 데이터 단위를 비트가 아닌 1byte단위로 추상화를 합니다. 따라서 메모리에 값을 저장할 때 하나의 주소에 1byte씩 저장할 수 있다고 생각하면 됩니다.
  • 문제를 풀 때에는 Tag bit = m - s - b 라는 점은 변함이 없습니다. 다만 이제 단위가 bit가 아닌 byte라는 점을 기억해야 합니다.
  • 또한 설명을 하면서 지나친 부분이 있는데 블록 오프셋을 시작값으로 해서 얼마만큼의 데이터를 읽어올지를 결정하는 것은 시스템의 word 사이즈입니다. word 사이즈가 4bytes 인경우 4 byte를 읽어들인다고 생각하면 됩니다.

Direct Mapping

  • 우리가 지금까지 배운 캐쉬 구조를 Direct Mapping이라고 합니다.
  • Index는 set의 주소이고 Cache의 주소를 Tag라고 부릅니다. 여기에서는 1비트만 저장하는 캐쉬라고 보면 block Offset은 0이라고 생각해봅시다.
  • Data에는 Memory(10000)에 있는 값이 저장되었다고 보면 됩니다.
  • Valid가 필요한 이유는 캐쉬 블록에 값이 없는 경우에는 칸이 비어있는 것처럼 보이지만 사실 의미없는 0과 1의 값이 쓰레기값으로 들어가있습니다. 따라서 이런 값을 실제 데이터와 구분해주기 위해서 Valid를 표시하는 1비트가 필요합니다.

Direct Mapping의 단점

  • 위의 그림에서 메모리 주소인 m은 5비트로 이루어져 있고, Cache의 set의 개수가 8개(8칸) 이므로 S = 2 ^ 3, s = 3비트 입니다.
  • 캐시 한 칸이 차지하는 정보는 B = 1 byte= 2 ^ 0 byte 이니 Tag 비트 = m - s - b = 2bit라는 것을 알 수 있습니다.
  • 그림에서 보는 것처럼 다른 Cache의 비어있는 set이 있더라도 각 메모리 주소가 들어갈 수 있는 칸이 정해져 있기 때문에 2개의 칸에만 계속해서 값이 저장되는 것을 볼 수 있습니다.
  • 캐시는 공간 활용을 잘 하지 못해 miss rate이 높아질 거라고 예상할 수 있습니다.

Set associate Cache

  • 이름을 듣고 어려워 보일 수 있지만 그렇지 않습니다. 이전에 배웠던 Direct Mapping Cache는 메모리의 주소에 따라서 고정적으로 set이 정해지기 때문에 공간 활용을 잘 하지 못하는 것이 단점이라고 배웠습니다.
  • 그렇다면 어떻게 해결할 수 있을까요. 캐시가 값을 저장할 때 상황에 따라 값을 배정할 수 있다면 더 나을 것 같습니다.
  • 그래서 이전에는 하나의 Set에 하나의 Block만 있었던 것을 여러개의 Block이 Set에 들어갈 수 있도록 늘려줍니다. set안에 있는 블록의 수를 Line이라고 합니다. 지금까지는 Line = 1인 캐쉬만 만들었다고 볼 수 있습니다.
  • 그렇다면 setoffset이나 blockoffset을 만든 것처럼 lineoffset이 필요할까요?
  • 아닙니다. lineoffset을 만들어준다면 lineoffset비트에 따라서 고정적으로 위치가 정해질 테니 만들어준 의미가 없겠죠. 그래서 tag bit = m - s - b라는 공식은 변하지 않습니다.
  • 이제 같은 set에 메모리 값이 여러개가 저장되려고 할 때 우리는 하나의 set안에 복수의 line을 넣음으로써 캐시에게 같은 set안에서 어떤 위치에 값을 저장할 지 자율성을 선사한 셈입니다.
  • 자 설명이 길었는데 그림으로 보겠습니다.
  • Direct Mapping과 비교해서 Cache의 자율권이 늘어난 것이 보이시나요. 자율성이 늘어나면서 캐시는 정책이 필요해졌습니다. 어떻게하면 cash miss를 줄일 수 있을까요?
  • 연속적으로 같은 set에 서로 다른 값들이 저장되려고 할 때 새로 들어온 값을 어디에 배치할 것인지에 대한 문제는 기존의 저장되있던 어떤 캐시의 값을 삭제할 것인지와 필연적으로 맞닿아 있습니다.
  • 또한 cpu가 보내준 주소값의 cache hit을 확인하려고 할 때 set안에 여러개의 block이 있고 주소를 가지고는 그 중 어떤 블록에 값이 담겨있을지 전혀 예측할 수 없다는 단점도 생기게 되겠죠. 그래서 해당 set안의 모든 block(line개수와 같겠죠)에 대해서 tag를 비교해서 값을 찾아내야 합니다.

Full associate Cache

  • Full associate cache는 한 줄로 설명할 수 있습니다.
  • set이 감소하고 line이 늘어나던 associate cache가 최대로 팽창한 1개의 set안에 모든 블록이 들어있는 cache입니다.

Cache의 정책

  • 어떤 캐쉬값을 삭제할 것인가.

Cache Miss

  • 일부러 C로 앞글자를 맞추었는지 모르겠지만 모두 다 C로 시작한다.
  • Compulsory Miss : Cash가 채워지지 않아서 발생하는 Miss
    • Block Size를 크게 함으로서 줄일 수 있다
    • Block Size를 크게 함으로써 Miss penalty가 커질 수 있다.
  • Conflict Miss : Cash의 같은 블록에 서로 다른 값이 충돌할 수 있어서 발생하는 Miss
    • set Associate를 늘임으로써 어느정도 해결이 가능하다.
    • set이 증가하면서 Access time(hit time)이 증가하게 된다.
  • Capacity Miss : 프로그램에서 필요한 메모리의 크기가 Cache의 용량보다 크기 때문에 발생하게 되는 MISS
    • 당연히 캐쉬의 용량의 크기를 키우면 해결된다.
    • 큰 캐쉬는 Access time(hit time)을 증가시킬 수 있다.

Write

  • Store instruction은 CPU에서 계산한 값을 메모리의 해당 주소에 저장하는 기능을 수행합니다.
  • 이 경우 Cache에 해당 주소가 있을 경우와 없는 경우로 나눌 수 있습니다.

캐쉬에 주소가 있는 경우

  • Write-through : 캐쉬에도 쓰고 메모리에도 쓰는 방법입니다. 이 경우 매번 메모리에 쓰는 작업은 큰 비효율을 초래하기 때문에 Write buffer라는 공간에 모아두었다가 Write buffer가 꽉 차면 한번에 업데이트합니다.
  • Write-back : 캐쉬에만 써두었다가 나중에 캐쉬에서 밀려날 때 마지막 값을 메모리에 저장을 하는 방식입니다.

캐쉬에 주소가 없는 경우

  • Write allocation : 메모리 값에 값을 저장한 후에 캐쉬에도 가져옵니다.
  • no Write allocation : 메모리에만 값을 저장합니다.

세부 Cache의 핵심 역할

  • Intel Architecture는 하나의 Cache로 존재하는 것이 아니라 L1, L2, L3와 같이 여러개의 세부 Cache들로 구성된다.
  • L1, L2, L3 순으로 Cache에서 가까운데 L1, L2 Cache의 역할은 hit time을 줄이는 것이다. 대부분이 hit이 되기 때문에 hit time이 줄어드는 것이 중요하다.
  • L3의 역할은 어느정도 hit time이 느려지더라도 Memory까지 내려가는 걸 필사적으로 막아야한다. miss rate시에 Memory를 참조하는 penalty가 상당히 크기 때문에 따라서 miss rate을 줄이는 것을 핵심 목표로 한다.
  • 따라서 Set Associate의 way개수를 살펴보면 L1, L2는 8way, L3는 16way인 것을 알 수 있다.

Access Time

Cache의 성능은 Access Time으로 평가한다.

  • Access Time = Hit Time + Miss rate * Miss penalty
  • Hit time이 1 Cycle, Memory Access Time이 100 Cycle 이라고 할 때 hit rate가 97%, 99%인 두 개의 Cache의 성능을 비교해보자.
  • 97% Cache Access Time = 1 + 0.03 * 100 = 4 Cycle
  • 99% Cache Access Time = 1 + 0.01 * 100 = 2 Cycle
  • hit rate만 보았을 때는 비슷할 것 같았는데 실제 계산해보면 99% Cache가 97% Cache보다 두 배가 빠르다.
  • 따라서 Cache의 성능을 말할 때는 보통 Miss rate으로 얘기한다.

댓글

댓글 쓰기

이 블로그의 인기 게시물

[Linux, Unix] export, echo 명령어 알아보기

[Linux, Unix] export, echo 명령어 알아보기 export 그리고 echo 명령어 유닉스 환경에서 개발을 하다보면 export와 echo라는 명령어를 종종 사용하게 됩니다. 간단하게 정리하려고 합니다. 유닉스를 사용한다면 Bash, ZSH라는 이름을 많이 들어보셨을 텐데요. Bash와 Zsh는 쉘 스크립트 언어를 말합니다. 터미널을 키면 그 터미널이 동작하는 방식을 결정하는 것이 쉘 스크립트 언어입니다. 변수와 echo 우리가 알아볼 것은 운영체제 변수와 쉘 변수 입니다. 운영체제 변수는 우리 프로그램이 돌아가는 운영체제의 변수를 말하는 것이 쉘 변수는 터미널 내에서 변수를 말하는 것입니다. water = "삼다수" 명령어를 터미널에서 입력한다면 water라는 쉘 변수를 만드는 것이 됩니다. echo 명령어는 변수를 출력하는 프린트 함수인데요. 다음과 같이 입력하면 water에 저장된 값을 터미널에 출력합니다. 만약 $를 빼고 출력한다면 문자열을 출력하는 것으로 받아들여 water를 그대로 출력하게 됩니다. echo $water unset water unset 명령어는 변수를 삭제하는 역할을 하지요. 내 컴퓨터가 어떤 쉘 스크립트 언어를 사용하는지 궁금하면 bash echo $SHELL 명령어를 통해서 어떤 쉘 스크립트 언어를 사용하고 있는지 알 수 있습니다. 지금까지의 변수들은 쉘 변수들을 다루어 보았구요. 이제 운영체제 변수에 대해서 알아보도록 할게요. env 위의 명령어를 입력하게 되면 운영체제 변수들을 출력하게 됩니다. 모든 프로그램은 운영체제위에서 돌아가기 때문에 운영체제 변수를 다른 말로 환경변수라고도 합니다. export export 명령어를 통해서 쉘 변수를 환경변수로 저장할 수 있는데요. export water 터미널에 위 명령어를 입력하고 env 라고 입력하면 환경변수 목록에 water가 추가되었음을 확인할 수 있습니다. 하지만 이
자세한 내용 보기

뼈속 깊이 이해하기 :: 1. 허프만 코딩

이미지
뼈속 깊이 이해하기 :: 1. 허프만 코딩 시작하면서 인터넷에 허프만 코딩을 검색하면 허프만 코딩은 상당히 쉽다고 설명하면서 허프만 트리를 그려놓고 있다. 그렇지만 어떤 이론도 처음 창안해내는 사람의 관점에서 생각하기는 쉽지 않은 일이다. 지식은 창시자를 떠나 많은 사람을 거쳐서 배울 수록 이해가 아닌 암기가 되기 싶다. 그래서 암기하기 쉬운 지식을 쉬운 지식이라고 말하고 있지는 않은가 싶다. 많은 어려운 이론들을 배우지만 아주 사소한 것도 생산하지 못하는 학생이 되는 것을 경계한다. 그런 관점에서 허프만이 되어 허프만 코딩을 뼈속 깊이 이해하는 것은 쉽지 않은 것 같다 사전 지식 컴퓨터가 정보를 전달하기 위해서는 텍스트를 0과 1로 이루어진 숫자 조합을 보내고 받는 쪽에서 이를 해석해 다시 텍스트로 바꾸는 과정이 필요하다. 고정 길이 코드 란 고정된 크기만큼의 비트를 사용해서 정보를 인코딩해서 보내는 인코딩방식이다. 우리가 알고있는 ASCII, UNICODE가 이에 해당한다. ASCII는 8비트를 사용해서 인코딩하고 UNICODE는 더 큰 비트를 사용한다. 접두어 코드(Prefix-code) 란 한 코드가 다른 코드의 앞부분이 되는 인코딩 방식이다. 예를 들어 모스 부호는 알파뱃 S를 "· · ·"로 , 알파뱃 E를 "·"로 인코딩한다. 따라서 알파뱃 E를 표현하는 "·"는 알파뱃 S를 표현하는 "···"의 앞부분과 완전히 일치한다. 이 경우 "···"코드를 전달할 때는 코드를 전달받는 사람이 (· · ·)를 EEE가 아닌 S로 해석하기를 기도해야 한다. 이와 같이 접두어 코드는 일련의 코드 조합이 의도하지 않은 방향으로 해석될 수 있는 해석의 어려움을 갖는다. Prefix-free-code 란 한 코드가 다른 코드의 접두어가 되지 않는 코딩방식이다. 우리가 오늘 다룰 주제인 허프만 코딩이 그 대표적인 방법이다. {
자세한 내용 보기

IEEE 754 부동 소수점 반올림과 근사

이미지
컴퓨터는 단지 숫자다 :: 2. 부동 소수점 반올림과 Rounding 컴퓨터는 단지 숫자다 :: 근사와 Rounding 부동 소수점 표현법 이전 포스팅 보기 서론 프로그래밍 언어는 어떤 언어든지 완전하지 못하다. 이번 파트에서는 프로그램 언어가 가지는 태생적인 결함 중에서 근사에 대한 얘기를 해보려고 한다. 플라톤은 자신의 철학 사상을 얘기하면서 '이데아’를 주장하였다. 사람이 그린 어떤 삼각형도 모든 내각의 합이 결코 정확한 180도가 될 수 없지만 세상 밖에서는 모든 내각의 합이 정확히 180도인 삼각형의 원형이 존재한다는 사상이었다. 컴퓨터마저도 수를 표현함에 있어 '이데아’를 실현하지는 못한다. 예를 들어 0.1이라는 수를 컴퓨터는 정확히 표현할 수 없어 0.10000000000000000555111512... 이라는 값으로 저장한다. 정밀도에 따라 32비트 혹은 그 이상이 될 수 있겠지만 중요한 것은 컴퓨터도 때로는 정확한 값을 저장할 수 없다는 말이다. 이러한 오차는 별 것 아니라고 생각할 수 있겠지만 제대로 컨트롤 하지 못하는 수의 오차는 생각보다 심각한 문제를 일으키기도 한다. 1991년 2월 25일 1차 걸프 전쟁 기간중 사우디아라비아 Dharan에 위치한 미국 패트리엇 미사일 부대는 날아오는 이라크의 스커드 미사일을 격추하는 데 실패해 28명의 대원이 사망 했다. 미국 조사위는 이 실패에 관해 상세한 조사를수행한 결과 수치 계산의 부정확성이 주요 원인이라는 결론을 내렸다. 패트리엇 시스템은 내부적으로 0.1초마다 증가하는 카운터가 있었고 0.1초를 내부적으로 24비트에 저장해 근사값으로 더하고 있었다. 이 때 0.1초의 오차는 2 − 2 0 × 1 1 0 2^{-20}\times{1\over10} 2 − 2 0 × 1 0 1 ​ 이었고 약 100시간동안 패트리어트 시스템이 동작하고 있었고 스커드 미사일이 2000m/s로 날아오고 있었다. 그 결과 격추 시스템의 오차는 약 6
자세한 내용 보기